11. State Machine Properties
Systems that can be modeled as finite state machines will tend to have context-specific behaviours to validate. What is expected in one state may not be desirable in another one, and trying to model all state transitions into a single larger property would prove annoyingly complex. A special type of stateful tests can be written specifically as state machines, where state names and transitions are made into first-class citizens, allowing to properly explore their expected transitions.
That type of test will be specifically useful when the user of the system can interact with it while perceiving multiple states, as opposed to just knowing that the system has a state machine internally. To put it another way, state machine properties are for when the model itself is a state machine, not the system. If there are no specific discernible states for the user—and therefore no specific discernible states for the model—then regular stateful properties are more appropriate.
11.1. Basics
The components for state machine tests are the same as those for stateful tests:
-
the model
-
the generation of commands representing the execution flow
-
the validation of the system against the model
They are, however, subtly different. The model is made of three parts:
-
A data structure representing the expected state of the system (the data it holds)
-
An initial state name, either an atom or a tuple, representing the state of the model (the finite state machine’s state name)
-
A series of functions that transform the model state based on operations that could be applied to the system, representing its changes when executed
The generation of commands is where the largest difference stands:
-
A list of functions sharing the name of the states, each of which returns a list of symbolic calls with generators defining their arguments, along with the name of the next state to transition to
-
A series of preconditions that define whether a given symbolic call would make sense to apply according to the current model state
-
An optional call that defines the probability of a given state transition to happen; if no weight is defined, all transitions are equally likely
Finally, there is the validation of the system against the model. Those are similar to stateful tests postconditions, but they also include information about the model’s state transition.
11.2. Execution Model
The execution of a state machine test is divided in two phases, one abstract and one real, similar to stateful tests. The abstract phase is used to create a test scenario, and is executed without any system code running.
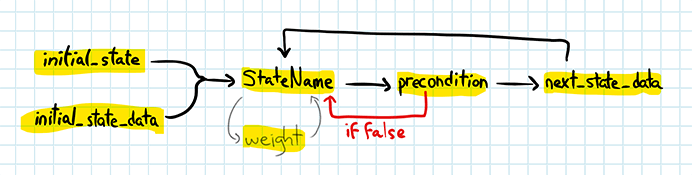
The initial state and data are used to pick the first StateName function to be called in abstract mode, possibly modified by the weight function. The precondition is used to validate whether the command is suitable. If unsuitable, generation starts over again at the StateName level until a suitable one is found. Once a suitable command is found, the state transition for this command is applied to the model state, and the next command is generated in a similar manner, but with StateName chosen based on the previous command’s setting. The framework is in charge of choosing when to stop based on the desired complexity. Once the process is over, a valid and legitimate sequence of commands will have been generated.
Once a command sequence is in place, the actual execution can take place:
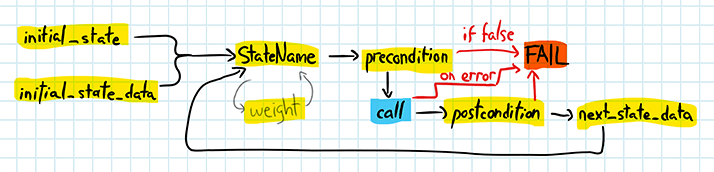
The execution phase runs the generated command sequence against the real system. The preconditions are still re-evaluated to ensure consistency so that if a generated precondition that used to work suddenly fails, the entire test also fails. The next symbolic call in the list is executed, with its result stored. The postcondition is then evaluated, and if it succeeds, the state transition for the command is applied to the state and the next command can be processed.
11.3. Structure of Properties
As with stateful tests, the structure of state machine properties may vary from project to project, but a common set of functionality intersects all of them:
-module(prop_fsm).
-include_lib("proper/include/proper.hrl").
-export([initial_state/0, initial_state_data/0,
on/1, off/1, service/3 (1)
weight/3, precondition/4, postcondition/5, next_state_data/5]).
prop_test() ->
?FORALL(Cmds, proper_fsm:commands(?MODULE), (2)
begin
actual_system:start_link(),
{History,State,Result} = proper_fsm:run_commands(?MODULE, Cmds), (3)
actual_system:stop(),
?WHENFAIL(io:format("History: ~p\nState: ~p\nResult: ~p\n",
[History,State,Result]),
aggregate(zip(proper_fsm:state_names(History),
command_names(Cmds)), (4)
Result =:= ok))
end).
-record(data, {}).
%% Initial state for the state machine
initial_state() -> off. (5)
%% Initial model data at the start. Should be deterministic.
initial_state_data() -> #data{}. (6)
%% State commands generation
on(_Data) -> [{off, {call, actual_system, some_call, [term(), term()]}}]. (7)
off(_Data) ->
[{off, {call, actual_system, some_call, [term(), term()]}},
{history, {call, actual_system, some_call, [term(), term()]}}, (8)
{{service,sub,state}, {call, actual_system, some_call, [term()]}}]. (9)
service(_Sub, _State, _Data) -> (10)
[{on, {call, actual_system, some_call, [term(), term()]}}].
%% Optional callback, weight modification of transitions
weight(_FromState, _ToState, _Call) -> 1. (11)
%% Picks whether a command should be valid. (12)
precondition(_From, _To, #data{}, {call, _Mod, _Fun, _Args}) -> true.
%% Given the state states and data *prior* to the call `{call, Mod, Fun, Args}',
%% determine if the result `Res' (coming from the actual system) makes sense. (13)
postcondition(_From, _To, _Data, {call, _Mod, _Fun, _Args}, _Res) -> true.
%% Assuming the postcondition for a call was true, update the model
%% accordingly for the test to proceed. (14)
next_state_data(_From, _To, Data, _Res, {call, _Mod, _Fun, _Args}) ->
NewData = Data,
NewData.| 1 | Each state of the state machine has its own function to act as a command generator |
| 2 | The proper_fsm module exports its own commands/1 function to tie all generators together for state machines |
| 3 | It similarly exports its own run_commands/2 function for the execution of the state machine model |
| 4 | Outputting data after the test runs requires a bit more set up than for stateful tests; zip/2 is an auto-imported variant of lists:zip/2 made for PropEr’s output. |
| 5 | Finite state machine model’s initial state |
| 6 | Model’s initial data, should be deterministic |
| 7 | A call from this state will transition to the off state |
| 8 | A call with the history state will remain in the same state it already was |
| 9 | Nested states can be represented as a tuple |
| 10 | Special state callback format for nested states |
| 11 | Relative probability of specific state transitions to take place. If unspecified, all transition probabilities are equal. |
| 12 | Precondition. If it returns true to a given command, it will be used. Returning false will force a new attempt at generating a command. |
| 13 | Postcondition. The result of the actual system execution is in _Res. |
| 14 | Transition the model’s data. The value for _Res will be a symbolic placeholder during symbolic execution. Treat as an opaque value that cannot be modified. |
|
The two execution flows are important to keep in mind: since the calls to preconditions, state commands and transitions are executed both when generating commands and when running the actual system, side-effects should be avoided in the model. And any value coming from the actual system that gets transferred to the model should be treated as an opaque blob that cannot be inspected, be matched against, or be used in a function call that aims to transform it. As in stateful tests, actual system values will be replaced with placeholders during the symbolic phase. |
|
Erlang’s Quickcheck has different callbacks for this form of testing. They are logically equivalent, but the form is based on function names. See the eqc_fsm documentation for details. |
11.4. Testing a Circuit-Breaker
Klarna's circuit_breaker library implements a circuit breaker. Circuit breakers are used to detect errors recurring in a given system. If the frequency at which the errors happen is considered to be too high, the breaker is tripped. Once tripped, further calls automatically fail before having a chance to reach the subsystem gated by the breaker. The idea is that failures tend to be costly, take a lot of time, and that a failing system under heavy stress is even harder to get back into a usable state. The circuit breaker allows cheap and early failures for a quicker recovery.
11.4.1. Ground Work
The library has seen significant production use and has some unit tests, but nearly no documentation. One can define a tolerance of multiple errors per given period of time, including error values and timeouts for slow execution. If the threshold is crossed, the breaker trips. It can then be reset by waiting or manually clearing its status. There are also ways to manually trip the breaker to prevent any call from succeeding. For the sake of simplicity, the state machine model will not consider the time aspects of the circuit breaker in terms of recovery, but only the tripping and manual clearing of its state.
This gives three main states:
-
okstate, when the subsystem gated by the circuit breaker is assumed to be functional -
trippedstate, where too many failures have happened and calls are forced to fail by the breaker -
blockedstate, caused by manual intervention.
The circuit breaker interface is slightly complex:
circuit_breaker:call(
{myservice, SomeId}, (1)
fun() -> some_call(State) end, (2)
timer:minutes(1), (3)
fun() -> true end, (4)
timer:minutes(5), (5)
%% Options
[{n_error, 3}, (6)
{time_error, timer:minutes(30)},
{n_timeout, 3}, (7)
{time_timeout, timer:minutes(30)},
{n_call_timeout, 3}, (8)
{time_call_timeout, timer:minutes(25)},
{ignore_errors, [not_found]}] (9)
).| 1 | Service identifier for the circuit; a name to know for which subsystem the failures should be counted. |
| 2 | Function being monitored by the circuit breaker |
| 3 | A time duration, in milliseconds, after which the call is deemed to have timed out if it hasn’t yet returned. |
| 4 | After a circuit that was tripped is cleared again, this callback will be executed. Useful for side-effects. |
| 5 | Cooldown period for the breaker; the time to wait for once tripped before allowing further attempts. |
| 6 | Number of errors (returning {error, Term} or failing with an exception) tolerated per unit of time. |
| 7 | Number of timeouts (returning timeout as a value) tolerated per unit of time. Not tested in this chapter. |
| 8 | Number of call timeouts (taking too long to return) tolerated per unit of time |
| 9 | Error values that will be ignored towards the failure count, or considered successful. |
This is a relatively verbose interface. To abstract it away in the property, a shim module similar to the one used in the previous chapter will prove useful, and will also allow to enforce the same type of determinism:
-module(shim_break).
-export([success/0, err/1, ignored_error/1, timeout/0,
manual_block/0, manual_deblock/0, manual_reset/0]).
-define(SERVICE, test_service).
options() -> (1)
[{n_error, 3},
{time_error, timer:minutes(30)},
{n_timeout, 3},
{time_timeout, timer:minutes(30)},
{n_call_timeout, 3},
{time_call_timeout, timer:minutes(30)},
{ignore_errors, [ignore1, ignore2]}].
success() ->
circuit_breaker:call(
?SERVICE,
fun() -> success end, timer:hours(1), (2)
fun() -> true end, timer:hours(1),
options()
).
err(Arg) ->
circuit_breaker:call(
?SERVICE,
fun() -> {error,Arg} end, timer:hours(1), (3)
fun() -> true end, timer:hours(1),
options()
).
ignored_error(Reason) -> err(Reason). % same call (4)
timeout() ->
circuit_breaker:call(
?SERVICE,
fun() -> timer:sleep(infinity) end, 0, (5)
fun() -> true end, timer:hours(1),
options()
).
manual_block() -> circuit_breaker:block(?SERVICE). (6)
manual_deblock() -> circuit_breaker:deblock(?SERVICE).
manual_reset() -> circuit_breaker:clear(?SERVICE).| 1 | The options will be stable and kept the same across all calls. Three of each error trips the breaker, and the timers are made long enough that time-based reset of the breaker does not impact the test |
| 2 | The successful call simply works by returning success. |
| 3 | The argument to the error-provoking functions will cause a reported failure on every execution; circuit_breaker accepts this format, but an exception could also be raised within the caller without a problem. |
| 4 | Exact duplicate, but to be called by the system with ignored reasons (ignore1 or ignore2) |
| 5 | Timeout calls are created by waiting forever in the function, with a timeout of 0. |
| 6 | Manual calls, with a simpler interface. |
Even though the shim is often created after having started working on the property, it may make sense to do it first. In the current case, since the system being tested is likely to contain multiple complex interactions and has been mature for a long period of time, the act of creating the shim first allows to reduce the scope of the tests required. That smaller scope is useful to get a first FSM going, and could always be expanded later for an actual system.
11.4.2. First Model Attempt
The property itself can be written as follows, with very few changes from the default one:
-module(prop_break).
-include_lib("proper/include/proper.hrl").
-compile(export_all).
-define(DEFAULT_LIMIT, 3).
prop_test() ->
?FORALL(Cmds, proper_fsm:commands(?MODULE),
?TRAPEXIT( (1)
begin
{ok, Pid} = circuit_breaker:start_link(),
{History, State, Result} = proper_fsm:run_commands(?MODULE, Cmds),
gen_server:stop(Pid), (2)
?WHENFAIL(io:format("History: ~p\nState: ~p\nResult: ~p\n",
[History,State,Result]),
aggregate(lists:zip(proper_fsm:state_names(History),
command_names(Cmds)),
Result =:= ok))
end)
).| 1 | The ?TRAPEXIT macro can be used to prevent PropEr from imploding when the system under test may fail and kill the executing process. ?TRAPEXIT forces its contents to run in an isolated process monitored by the framework, transforming crashes into shrinkable test failures. |
| 2 | Knowing that a gen_server behaviour is at the core of the circuit breaker, this internal function can be used to force a clean shutdown even if none is provided out of the box. |
With all this in place, the model can be written.
-record(data, {
limit :: pos_integer(),
registered = false :: boolean(),
errors = 0 :: pos_integer(),
timeouts = 0 :: pos_integer()
}).
initial_state() ->
ok.
initial_state_data() ->
#data{limit = ?DEFAULT_LIMIT}.The only data required for the model is the limit of calls causing a failure—with a macro setting it to 3, in accordance to what was in the shim—and a counter for each type of error being handled. There is also a boolean registered field. This field is used to track whether a call has been made to the circuit breaker yet. The reason is that some calls, such as manual overrides, can only be valid if they are run on a service that has been called at least once before.
The state machine initially begins in the ok state, which should allow the following calls and transition:
ok(_Data) ->
[{history, {call, shim_break, success, []}},
{history, {call, shim_break, err, [valid_error()]}},
{tripped, {call, shim_break, err, [valid_error()]}},
{history, {call, shim_break, ignored_error, [ignored_error()]}},
{history, {call, shim_break, timeout, []}},
{tripped, {call, shim_break, timeout, []}},
{blocked, {call, shim_break, manual_block, []}},
{ok, {call, shim_break, manual_deblock, []}},
{ok, {call, shim_break, manual_reset, []}}].
[...]
%% Generators
valid_error() -> elements([badarg, badmatch, badarith, whatever]).
ignored_error() -> elements([ignore1, ignore2]).All the calls from the shim are represented in that list. A special thing to note is that calls to err/1 and timeout/0 are there twice each: once with a transition to the current (ok) state through the history atom, and once to the tripped state. That is because until a given error threshold is reached, the circuit breaker should not be tripped and therefore not cause a transition.
The tripped state has simpler transition rules:
tripped(_Data) ->
[{history, {call, shim_break, success, []}},
{history, {call, shim_break, err, [valid_error()]}},
{history, {call, shim_break, ignored_error, [ignored_error()]}},
{history, {call, shim_break, timeout, []}},
{ok, {call, shim_break, manual_deblock, []}},
{ok, {call, shim_break, manual_reset, []}},
{blocked, {call, shim_break, manual_block, []}}].Manually resetting and deblocking should both return to the ok state. Aside from that, nothing for this model will go back to normal of its own. If time were to be taken into account, a shim call to "wait for reset" could probably be added, but is out of scope at this time.
The blocked state is mostly identical:
blocked(_Data) ->
[{history, {call, shim_break, success, []}},
{history, {call, shim_break, err, [valid_error()]}},
{history, {call, shim_break, ignored_error, [ignored_error()]}},
{history, {call, shim_break, timeout, []}},
{history, {call, shim_break, manual_block, []}},
{history, {call, shim_break, manual_reset, []}},
{ok, {call, shim_break, manual_deblock, []}}].The only major distinction is that a manual block is stronger than a tripped state. Resetting the breaker will not exit a blocked state; only a manual deblocking operation will bring the state back to ok.
As in stateful tests, the command generation is not sufficient on its own to guarantee proper selection of commands when shrinking. Preconditions are required to tie down all the invariants to be respected by the state machine model:
%% Picks whether a command should be valid under the current state.
precondition(_From, _To, Data, {call, _, manual_reset, _}) -> (1)
Data#data.registered;
precondition(_From, _To, Data, {call, _, manual_block, _}) ->
Data#data.registered;
precondition(_From, _To, Data, {call, _, manual_deblock, _}) ->
Data#data.registered;
precondition(ok, To, #data{errors=N, limit=L}, {call,_,err,_}) -> (2)
(To =:= tripped andalso N+1 =:= L) orelse (To =:= ok andalso N+1 =/= L);
precondition(ok, To, #data{timeouts=N, limit=L}, {call,_,timeout,_}) ->
(To =:= tripped andalso N+1 =:= L) orelse (To =:= ok andalso N+1 =/= L);
precondition(ok, ok, _Data, _Call) -> (3)
true;
precondition(tripped, _, _Data, _Call) ->
true;
precondition(blocked, _, _Data, _Call) ->
true.| 1 | All manual calls are allowed only if the current breaker is registered, no matter the state |
| 2 | Calls to errors and timeouts from the ok state will be allowed only if they are transitioning (a) to the tripped state when the error counter passes the limit threshold, or (b) going back to the ok state when it does not do so. This prevents picking an invalid state transition for a given erroneous behaviour. |
| 3 | All other calls and transitions are deemed valid |
The state transitions attached to these follows:
%% Assuming the postcondition for a call was true, update the model
%% accordingly for the test to proceed.
next_state_data(ok, _To, Data=#data{errors=N}, _Res, {call,_,err,_}) -> (1)
Data#data{errors=N+1, registered=true};
next_state_data(ok, _To, Data=#data{timeouts=N}, _Res, {call,_,timeout,_}) ->
Data#data{timeouts=N+1, registered=true};
next_state_data(_From, _To, Data, _Res, {call,_,manual_deblock,_}) -> (2)
Data#data{errors=0, timeouts=0};
next_state_data(_From, _To, Data, _Res, {call,_,manual_reset,_}) ->
Data#data{errors=0, timeouts=0};
next_state_data(_From, _To, Data, _res, {call,_,manual_block,_}) ->
Data;
next_state_data(_From, _To, Data, _Res, {call, _Mod, _Fun, _Args}) -> (3)
Data#data{registered=true}. % all calls but manual ones register| 1 | erroneous calls and those that time out increment their respective counters |
| 2 | manual deblocking and clearing of the circuit breaker reset the model’s counters |
| 3 | All non-manual calls 'register' the circuit breaker, ensuring that after this action (based on preconditions), manual calls can happen without error |
The last thing to cover are postconditions, validating that the actual system complies with the model:
%% Given the state `State' *prior* to the call `{call, Mod, Fun, Args}',
%% determine whether the result `Res' (coming from the actual system)
%% makes sense.
postcondition(tripped, tripped, _Data, _Call, {error, {circuit_breaker, _}}) -> (1)
true;
postcondition(_, blocked, _Data, {call, _, manual_block, _}, ok) ->
true; (2)
postcondition(_, blocked, _Data, _Call, {error, {circuit_breaker, _}}) ->
true;
postcondition(_, ok, _Data, {call, _, success, _}, success) -> (3)
true;
postcondition(_, ok, _Data, {call, _, manual_deblock, _}, ok) ->
true;
postcondition(_, _, _Data, {call, _, manual_reset, _}, ok) -> (4)
true;
postcondition(ok, _, _Data, {call, _, timeout, _}, {error, timeout}) -> (5)
true;
postcondition(ok, _, _Data, {call, _, err, _}, {error, Err}) -> (6)
not lists:member(Err, [ignore1, ignore2]);
postcondition(ok, _, _Data, {call, _, ignored_error, _}, {error, Err}) ->
lists:member(Err, [ignore1, ignore2]);
postcondition(From, To, _Data, {call, _Mod, Fun, Args}, Res) ->
io:format("unexpected postcondition: ~p -> ~p ({~p,~p}) = ~p~n",
[From, To, Fun, Args, Res]),
false.| 1 | All calls that remain in a tripped state had to be failures (since the rest are manual overrides) |
| 2 | All calls that remain or transition to the blocked state failed, with the exception of the manual block call that brings the breaker into the blocked state to begin with |
| 3 | When a call ends in the ok state, it means that it was either in that state already, that it forced a transition to that state, or both. In the case of success, it was in that state; in the case of manual_deblock, both scenarios are valid. |
| 4 | Manual resetting always returns ok (as long as it was registered). |
| 5 | calls that can potentially cause the state machine to transition to the tripped state use the From argument to pattern match on ok instead. |
| 6 | Errors return what they were expected. |
Any other return value is declared as failing by default.
There is, by comparison with other stateful tests seen so far, fewer specific validations regarding the value returned, and a bigger focus on type. What the property at hand will really scrutinize is the fitness of the model—our high-level comprehension of how the system works—against the actual system—how the real thing operates in various contexts.
Running the tests will check whether everything holds up:
$ rebar3 proper
[...]
===> Testing prop_break:prop_test()
...............................................................
...unexpected postcondition: tripped -> tripped ({success,[]}) = success
!
Failed: After 67 test(s).
[...]
Shrinking unexpected postcondition: [...]
(8 time(s))
[{set,{var,9},{call,shim_break,err,[badarith]}},
{set,{var,12},{call,shim_break,err,[badarith]}},
{set,{var,13},{call,shim_break,ignored_error,[ignore1]}},
{set,{var,14},{call,shim_break,err,[badarg]}},
{set,{var,15},{call,shim_break,success,[]}}]
History: [{{ok,{data,3,false,0,0}},{error,badarith}},
{{ok,{data,3,true,1,0}},{error,badarith}},
{{ok,{data,3,true,2,0}},{error,ignore1}},
{{ok,{data,3,true,2,0}},{error,badarg}},
{{tripped,{data,3,true,3,0}},success}]
State: {tripped,{data,3,true,3,0}}
Result: {postcondition,false}
===>
0/1 properties passed, 1 failed
===> Failed test cases:
prop_break:prop_test() -> falseAnd things fail!
11.4.3. Debugging the Model
In the prior list of operations, the bad sequence of commands and states leading to the failure were:
unexpected postcondition: tripped -> tripped ({success,[]}) = success
[{set,{var,9},{call,shim_break,err,[badarith]}},
{set,{var,12},{call,shim_break,err,[badarith]}},
{set,{var,13},{call,shim_break,ignored_error,[ignore1]}},
{set,{var,14},{call,shim_break,err,[badarg]}},
{set,{var,15},{call,shim_break,success,[]}}]
History: [{{ok,{data,3,false,0,0}},{error,badarith}},
{{ok,{data,3,true,1,0}},{error,badarith}},
{{ok,{data,3,true,2,0}},{error,ignore1}},
{{ok,{data,3,true,2,0}},{error,badarg}},
{{tripped,{data,3,true,3,0}},success}]The way things look, three calls to an error should have tripped the system, but the call to success/0 still worked. According to the shrinking, the position of ignored errors appears to be important, since it would not be removed by shrinking. An easy guess would have been that the ignoring of errors does not work, but the problem case is opposite of that: the ignored error appears to allow more failures to happen without trouble.
The model does not correctly represent the system. Since the model thinks the breaker is tripped, the expected values do not match those of the real system. A back and forth of trying to reverse-engineer the model could ensue, but since circuit_breaker is open source, looking at the implementation can reveal the actual behaviour: any successful call will, in order, decrease the fault counter of the errors and call timeouts. That’s a bit odd and unexpected, but the model can be adapted:
next_state_data(ok, _To, Data=#data{errors=N}, _Res, {call,_,err,_}) ->
Data#data{errors=N+1, registered=true};
next_state_data(ok, _To, Data=#data{timeouts=N}, _Res, {call,_,timeout,_}) ->
Data#data{timeouts=N+1, registered=true};
next_state_data(ok, _To, Data=#data{errors=N, timeouts=M}, _Res,
{call,_,F,_}) when F == success; F == ignored_error -> (1)
if N > 0 -> Data#data{errors=N-1};
M > 0 -> Data#data{timeouts=M-1};
N =:= 0, M =:= 0 -> Data#data{registered=true}
end;
[...]The added clause ensures that error counters are properly decremented to represent the actual system, and also maintains registration rules in all cases.
Running the property succeeds, but has disappointing statistics:
===> Testing prop_break:prop_test()
....................................................................................................
OK: Passed 100 test(s).
14% {ok,{shim_break,err,1}}
14% {ok,{shim_break,timeout,0}}
9% {ok,{shim_break,success,0}}
9% {ok,{shim_break,ignored_error,1}}
7% {ok,{shim_break,manual_reset,0}}
6% {ok,{shim_break,manual_block,0}}
6% {ok,{shim_break,manual_deblock,0}}
4% {blocked,{shim_break,err,1}}
4% {blocked,{shim_break,manual_reset,0}}
4% {blocked,{shim_break,ignored_error,1}}
4% {blocked,{shim_break,manual_deblock,0}}
4% {blocked,{shim_break,timeout,0}}
3% {blocked,{shim_break,success,0}}
2% {blocked,{shim_break,manual_block,0}}
0% {tripped,{shim_break,success,0}}
0% {tripped,{shim_break,manual_block,0}}
0% {tripped,{shim_break,ignored_error,1}}
0% {tripped,{shim_break,timeout,0}}
0% {tripped,{shim_break,manual_deblock,0}}
0% {tripped,{shim_break,err,1}}
0% {tripped,{shim_break,manual_reset,0}}
===>
1/1 properties passedA bunch of calls are never used, mostly those in the tripped state. The new constraints likely make it hard to move there in the first place. The optional weight/3 callback can help:
weight(ok, tripped, _) -> 5;
weight(ok, ok, {call, _, F, _}) ->
case F of
error -> 4;
timeout -> 4;
_ -> 1
end;
weight(_, _, _) -> 1.The calls that are able to force a transition from ok to tripped are given a higher priority. In the case of a stable ok state, errors and timeouts are prioritized to also raise the chance of a transition to the tripped state. With this callback in place, metrics get in a better place:
===> Testing prop_break:prop_test()
....................................................................................................
OK: Passed 100 test(s).
28% {ok,{shim_break,timeout,0}}
17% {ok,{shim_break,err,1}}
4% {blocked,{shim_break,ignored_error,1}}
4% {blocked,{shim_break,err,1}}
3% {blocked,{shim_break,manual_reset,0}}
3% {blocked,{shim_break,success,0}}
3% {ok,{shim_break,success,0}}
3% {blocked,{shim_break,manual_block,0}}
3% {blocked,{shim_break,timeout,0}}
3% {ok,{shim_break,manual_block,0}}
2% {blocked,{shim_break,manual_deblock,0}}
2% {ok,{shim_break,ignored_error,1}}
2% {tripped,{shim_break,err,1}}
2% {tripped,{shim_break,success,0}}
2% {ok,{shim_break,manual_reset,0}}
2% {tripped,{shim_break,manual_deblock,0}}
1% {tripped,{shim_break,manual_block,0}}
1% {tripped,{shim_break,manual_reset,0}}
1% {tripped,{shim_break,ignored_error,1}}
1% {ok,{shim_break,manual_deblock,0}}
1% {tripped,{shim_break,timeout,0}}
===>
1/1 properties passedAnd then at least all types of transitions are tested.
With fairly minor modifications over stateful properties, systems that are better modeled as state machines can also be tested effectively.